12 Section 12. Extended topics
2021-12-02
12.1 Resources
- reading:
- end of BDA3 ch. 4
- optional: BDA3 ch. 8, 14-18, 21
- lectures:
- slides
12.2 Notes
12.2.1 Lecture 12.1 Frequency evaluation, hypothesis testing and variable selection
- Bayesian vs. Frequentist
- Bayesian theory has epistemic and aleatory probabilities
- Frequency evaluations focus on frequency properties given aleatoric repetition of an observation and modeling
- on “null hypothesis testing”:
- often inappropriate to test the probability that a value is 0
- for continuous data, the probability of a single value is always 0
- “region of practical equivalence” (ROPE) is another option
- best to focus on describing the full posterior
- e.g. amount of the posterior greater than or less than an important value
- e.g. where most of the posterior density is (89% or 95% HDI)
- often inappropriate to test the probability that a value is 0
- be careful about only looking at marginal posteriors, too
- joint posterior distributions may be informative
- e.g. height and weight variables in beta-blocker model are highly correlated; both marginals overlap 0, but joint does not
- most common statistical tests are linear models
- longer list with more illustrations: https://lindeloev.github.io/tests-as-linear
| classical test | Bayesian equivalent | in ‘rstanarm’ |
|---|---|---|
| t-test | mean of data | stan_glm(y ~ 1) |
| paired t-test | mean of diffs | stan_glm((y1 - y2) ~ 1) |
| Pearson correlation | linear model | stan_glm(y ~ 1 + x) |
| two-sample t-test | group means | stan_glm(y ~ 1 + gid) |
| ANOVA | hierarchical model | stan_glm(y ~ 1 + (1|gid)) |
12.2.2 Lecture 12.2 Overview of modeling data collection, BDA3 Ch 8, linear models, BDA Ch 14-18, lasso, horseshoe and Gaussian processes, BDA3 Ch 21
- LASSO and Bayesian LASSO
- Bayesian LASSO uses Laplace distribution as a prior
- is equivalent to L1 penalty in MLE LASSO, but because we still integrate over the entire posterior, it does not have the same “sparsifying” effect
- therefore, Bayesian LASSO is empirically worse than MLE LASSO
- final thought: best to separate the process of prior selection, posterior inference, and decision analysis
- regularized horseshoe prior a better choice if you have prior information that only some of the covariates are informative
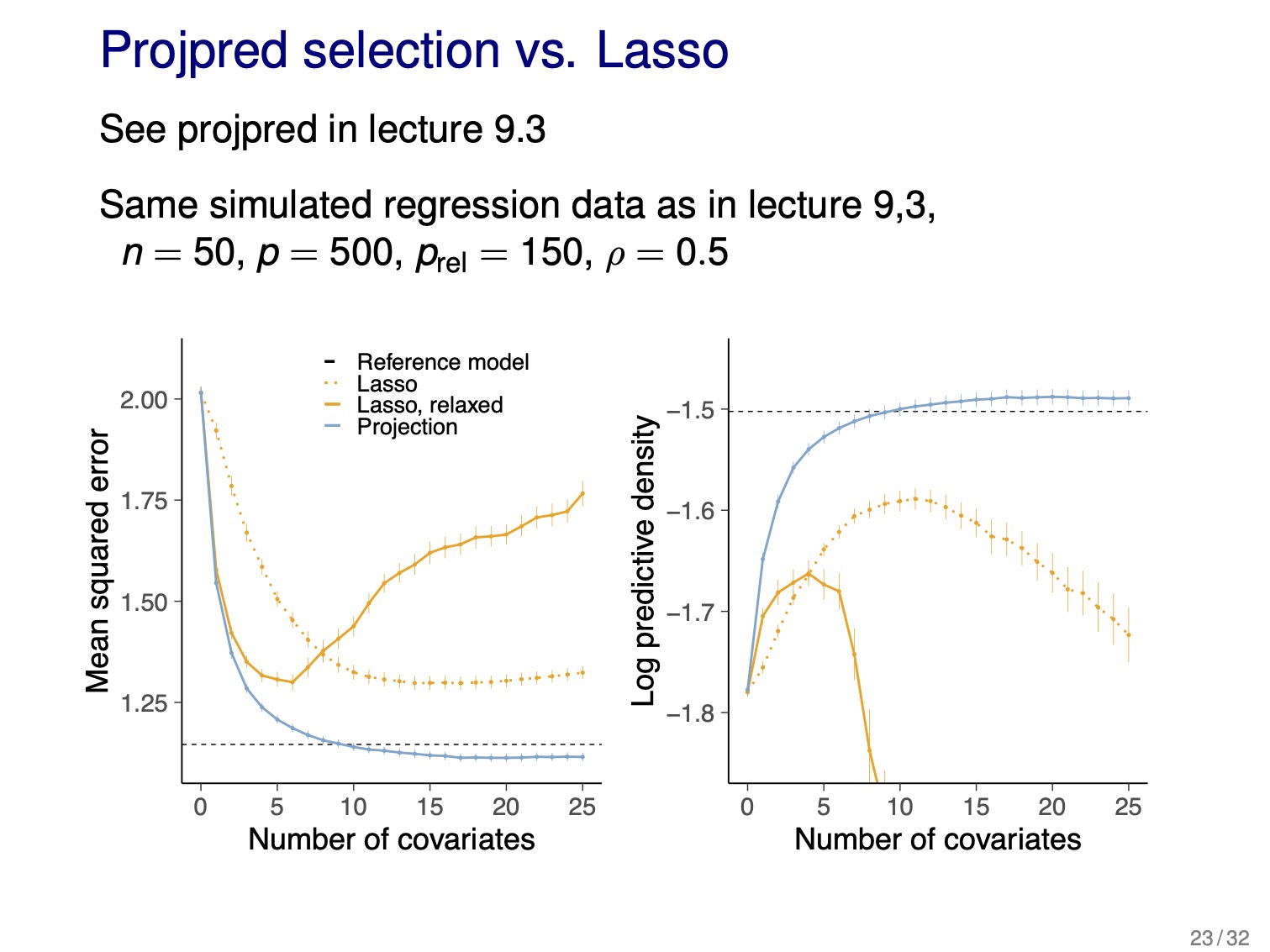
projpred selection vs LASSO